Hoy es marzo 14 o 3/14, también conocido como el Día de π (Pi) en recuerdo a los primeros tres dígitos de la expansión decimal del número irracional Pi.
Los matemáticos la tienen por "la constante del círculo" en términos del diámetro, al ser objeto de grandes usos para la investigación, cálculos de fenómenos y nuevas ecuaciones. Sin embargo, de acuerdo a varios matemáticos radicales, la verdadera constante es el radio de un círculo, mas no su diámetro. Por esto, ellos han denominado a este día como el "El día de un medio de Tau" donde Tau es la constante 2Pi.
Ellos explican que Tau tiene una mayor importancia que Pi en la trigonometría, la identidad de Euler e incluso las famosas fórmulas para obtener áreas como la del círculo al multiplicar Pi por radio al cuadrado.
Ellos explican que Tau tiene una mayor importancia que Pi en la trigonometría, la identidad de Euler e incluso las famosas fórmulas para obtener áreas como la del círculo al multiplicar Pi por radio al cuadrado.
Como datos curiosos:
- En la primera película de Futurama de Matt Groening, creador de Los Simpson, durante una conferencia de matemáticas, el orador pregunta a la audiencia llena de doctores en la materia, cuántos dígitos de Pi conocen. Matt Groening se levanta y comienza a decir los números correctos y luego una serie de dígitos sin sentido antes de terminar con 333 y decir "y después siguen un montón de 3's más".
- En Nueva York hay una calle que se llama la π th Avenida.
- Daniel Tammet tiene el récord europeo al recitar 22 mil 514 dígitos de Pi de memoria.
- La Biblia tiene una primitiva referencia respecto al número en el libro 1 Reyes Capítulo 7 versículo 23: "Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos."
- Adrian Paenza comparte un increíble experimento de Louis de Buffon para calcular Pi. El método se conoce con el nombre de "El problema de la Aguja de Buffon". Fue investigado en 1777 por el naturalista y matemático francés Comte Georges Louis de Buffon (1707-1788). Necesitamos algunos elementos (no muchos): consiga unos fósforos y sáqueles la cabeza o bien consiga palillos o agujas para coser. En una hoja de papel, dibuje líneas paralelas (como si fueran renglones), separadas unas de otras al doble de la medida de las agujas o de los palillos. Ahora, deje caer cada aguja sobre la hoja de papel, desde unos 30 centímetros de altura (aproximadamente). Cuente el número de agujas que o bien tocan o bien cruzan una de las líneas que usted dibujó. Y ahora, cuando terminó de soltar todos los agujas, haga el siguiente cálculo: "divida el número de agujas que tiró por la cantidad que o bien tocan o bien cruzan una de las líneas".
El número que obtenga es una aproximación al número (2/ pi). Naturalmente, cuantas más agujas intervengan en el experimento, mayor es la precisión con la que le permitirá calcular el valor de Pi.
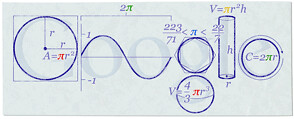
- El año pasado, Google colocó un Doodle especial y bastante elaborado para esta ocasión.
- En Nueva York hay una calle que se llama la π th Avenida.
- Daniel Tammet tiene el récord europeo al recitar 22 mil 514 dígitos de Pi de memoria.
- La Biblia tiene una primitiva referencia respecto al número en el libro 1 Reyes Capítulo 7 versículo 23: "Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo; su altura era de cinco codos, y lo ceñía alrededor un cordón de treinta codos."
- Adrian Paenza comparte un increíble experimento de Louis de Buffon para calcular Pi. El método se conoce con el nombre de "El problema de la Aguja de Buffon". Fue investigado en 1777 por el naturalista y matemático francés Comte Georges Louis de Buffon (1707-1788). Necesitamos algunos elementos (no muchos): consiga unos fósforos y sáqueles la cabeza o bien consiga palillos o agujas para coser. En una hoja de papel, dibuje líneas paralelas (como si fueran renglones), separadas unas de otras al doble de la medida de las agujas o de los palillos. Ahora, deje caer cada aguja sobre la hoja de papel, desde unos 30 centímetros de altura (aproximadamente). Cuente el número de agujas que o bien tocan o bien cruzan una de las líneas que usted dibujó. Y ahora, cuando terminó de soltar todos los agujas, haga el siguiente cálculo: "divida el número de agujas que tiró por la cantidad que o bien tocan o bien cruzan una de las líneas".
El número que obtenga es una aproximación al número (2/ pi). Naturalmente, cuantas más agujas intervengan en el experimento, mayor es la precisión con la que le permitirá calcular el valor de Pi.
- El año pasado, Google colocó un Doodle especial y bastante elaborado para esta ocasión.

Y tú ¿cuántos dígitos de la expansión puedes memorizar?...





No hay comentarios:
Publicar un comentario